Wer hat den KÃĪse zum Bahnhof gerollt?
Mit Eiern wird es schwieriger! Rollkurven an Kreis und Ellipse
 Bild: JÞrgen Daum
Bild: JÞrgen DaumProf: Angela Schwenk aus dem Studiengang Angewandte Mathematik
Schulfach:Mathematik
Variante 1: 45 min; reine Beobachtungen an abrollenden Kreisen und Ellipsen (Kreis auf Gerade, Kreis auf Kreisen)
Vorkenntnisse der Teilnehmer: keine
Variante 2: 90 min; Beobachtungen mit zugehÃķrigem mathematischen Hintergrund. Es wird eine Formel hergeleitet, die die Rollbewegung allgemeiner Kurven beschreibt.
Vorkenntnisse der Teilnehmer: Parameterdarstellung von Kurven in der Ebene, Ableitung, komplexe Zahlen
Teilnehmerkreis: ab 7. Klasse
BenÃķtigte AusrÞstung: Beamer (PC wird mitgebracht)
Inhalt
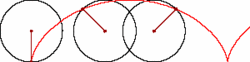

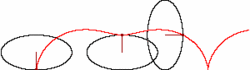
Rollkurven von Kreisen kommen im tÃĪglichen Leben vor: Ein Rad rollt auf der StraÃe, Sie beobachten einen festen Punkt des Reifens. Die Bahnkurve dieses Punktes ist eine sogenannte Zykloide. Dabei ist es im Prinzip egal, welcher Punkt auf dem Rand des Reifens beobachtet wird.
Doch wie sehen die Bahnkurven von Punkten auf rollenden Ellipsen aus? Wirkt sich die Wahl des beobachteten Punktes auf die Form der Bahnkurve aus? Entlang welcher Kurven bewegen sich Punkte, die innerhalb der Ellipse bzw. auÃerhalb befestigt sind?
KÃķnnen auch eckige RÃĪder rollen? Wie mÞsste eine StraÃe aussehen, damit man mit eckigen RÃĪdern komfortabel fahren kann?
Praktische Experimente liefern unter UmstÃĪnden wochenlang RÞhreier fÞr den Speiseplan. Theoretische Antworten auf all diese Fragen kann ein Mathematik-Programm, z. B. MathematicaÂŪ, liefern.
